Kongruenz

Aufgaben

1.: Gegeben sind folgende drei Dreiecke: MNO   RQP und RQP   UTS.

Begründe, warum  MNO   UTS ist !

Lösung:

1.Lösungsmöglichkeit:

Das Dreieck MNO ist deckungsgleich mit RQP und RQP ist deckungsgleich mit UTS und UTS ist deckungsgleich mit MNO. Daraus folgt, daß MNO und UTS kongruente Dreiecke sind.

2.Lösungsmöglichkeit:

Voraussetzung: MNO   RQP

RQP   UTS

Behauptung: MNO  UTS

Aussage: Begündung:

1.)  MNO   RQP und

RQP   UTS laut Voraussetzung

2.) [M,R] = [R,Q] [R,Q] = [U,T] zwei Dreiecke sind kongruent, wenn die

[N,O] = [Q,P] [Q,P] = [T,S] entsprechenden Seiten und

[M,O] = [R,P] [R,P] = [U,S] Winkel gleich sind

M =  R  R =  U

N =  Q  Q =  T

O =  P  P =  S

3.) [M,N] = [U,T]  M =  U

[N,O] = [T,S]  N =  T gilt wegen der Transitivität

[M,O] = [U,S]  O =  S

4.)  MNO   UTS da die Seiten und Winkel der beiden Dreiecke gleich sind, sind die Dreiecke kongruent

Bemerkung: Man könnte auch mit den Seiten allein arbeiten und den SSS - Satz anwenden.

Lösung:

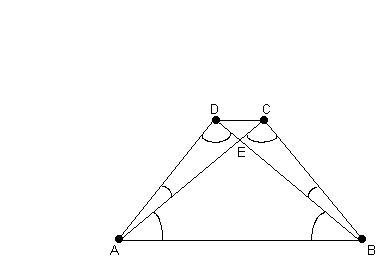
1.) ADC  BCD

2.) ADB  BCA

3.) DCE  ABE

Begründung zu 1.: Die zwei Dreiecke sind deckungsgleich, oder mit dem SWS - Satz.

Begründung zu 2.: Die zwei Dreiecke sind deckungsgleich, oder mit dem SWS - Satz.

Begründung zu 3.: Man führt zwei Hilfswinkel CDE und DCE ein, die sind genau so groß wie EAB und EBA. Weiters kann man der Figur entnehmen, daß die Winkel AEB und DEC Scheitelwinkel sind und daher gleich groß sind. D.h. die beiden Dreiecke DCE und ABE sind aufgrund des WWW - Satzes ähnlich.

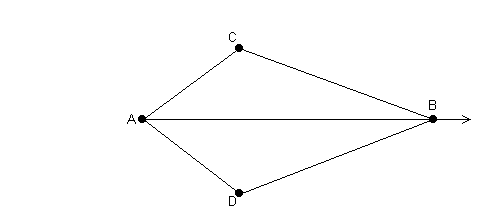
3.: In der folgenden Figur ist  =  und die Gerade AB ist die Winkelsymmetrale des Winkels CAD.

Begründe, daß  ABC   ABD ist.

Lösung:

Voraussetzungen:  = , AB ist die Winkelsymmterale des Winkels CAD

Behauptung:  ABC   ABD

Beweis:

Aussage: Begründung:

1.)  =  laut Voraussetzung

2.) Die Gerade AB ist die Winkelsymmetrale laut Voraussetzung

des Winkels CAD

4.)  CAB =  BAD Die Winkelsymmetrale teilt

den Winkel CAD in zwei

gleich große Winkel

5.) Die beiden Dreiecke stimmen folgt aus 1.) und aus

in zwei Seitenlängen überein der Figur entnimmt man,

daß zu beiden Dreiecken

die Seite AB gehört

6.)  ABC   ABD folgt aus 4.) und 5.)

mit Hilfe des SWS - Satzes

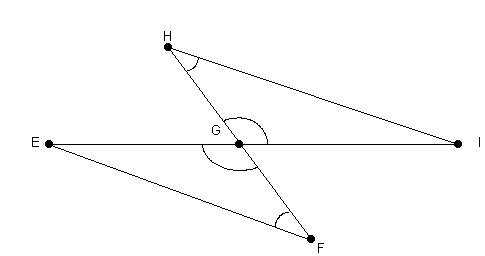
4.: In der folgenden Figur sind  und  Scheitelwinkel, G ist der Mittelpunkt der Strecke [H,F] und .

Der folgende Beweis zeigt, daß  =  ist. Fülle die Beweislücken!

Voraussetzungen:  und  sind Scheitelwinkel

G ist der MP der Strecke [H,F]

Behauptung:  = 

Beweis:

Aussage: Begründung:

1.) da Scheitelwinkel gleich groß sind

2.)  = 

3.) 

4.) die beiden Dreiecke haben zwei gleich große Winkel und eine gleich lange Seite,

daher folgt aus dem WSW - Satz,

daß die beiden Dreiecke kongruent sind.

5.) aus 4.) folgt, daß die beiden Dreiecke

deckungsgleich sind und

deshalb gilt die Behauptung.

Lösung:

Beweis:

Aussage: Begründung:

1.)  da Scheitelwinkel gleich groß sind

2.)  =  der Mittelpunkt G teilt laut Voraussetzung die Strecke [H,F] in zwei gleich lange Strecken

3.)  laut Voraussetzung

4.) GHI  GFE die beiden Dreiecke haben zwei gleich große Winkel und eine gleich lange Seite,

daher folgt aus dem WSW - Satz,

daß die beiden Dreiecke kongruent sind.

5.)  =  folgt aus 4.)

5.: In der folgenden Figur gilt:  =  und  = . Begründe, warum die Winkel ATU und ABU gleich groß sind !

Lösung:

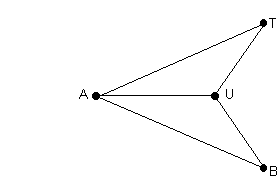
Aus der Figur entnimmt man, daß die Dreiecke  AUT und  AUB die Seite AV gemeinsam haben. Die beiden Dreiecke haben somit drei gleich lange Seiten und sind kongruent. Daraus folgt, daß auch die Winkel gleich groß sind, also insbesondere gilt, daß  ATU =  ABU ist.

6.: In der folgenden Figur gilt:  und  = . Der folgende Beweis zeigt, daß die Gerade TI die Winkelsymmetrale des Winkels FTA ist. Begründe die Beweisschritte!

Voraussetzung:  und  = 

Behauptung: TI ist die Winkelsymmetrale des Winkels FTA

Beweis:

Aussage: Begründung:

1.) 

2.) ' = 

' = 

3.) ' = '

4.)  = 

5.) Die beiden Dreiecke FIT und AIT

haben zwei gleich lange Seiten und

der eingeschlossene Winkel ist

gleich groß.

6.)  FIT   AIT

7.) 

8.) Die Gerade TI ist die Winkelsymmetrale

des Winkels FTA

Lösung:

Aussage: Begründung:

1.)  laut Vorausetzung

2.) ' =  aus der Figur kann man entnehmen, daß

' =   und ', sowie  und '

Supplementärwinkel sind

3.) ' = ' folgt aus 1.) und 2.)

4.)  =  laut Vorausetzung

5.) Die beiden Dreiecke FIT und AIT das erste entnimmt man der Figur

haben die Seite TI gemeinsam und und  = 

stimmen in einer weiteren

Seitenlänge überein

6.)  FIT   AIT folgt aus 5.), wenn man den

SWS - Satz anwendet

7.)  da die beiden Dreiecke kongruent sind,

müssen auch die Winkel

gleich groß sein

8.) Die Gerade TI ist die Winkelsymmetrale da die Gerade TI den Winkel FTA

des Winkels FTA in zwei gleich große Winkel teilt

7.: In der folgenden Figur gilt:  und  = . Der folgende Beweis zeigt, daß  = . Fülle die Beweislücken !

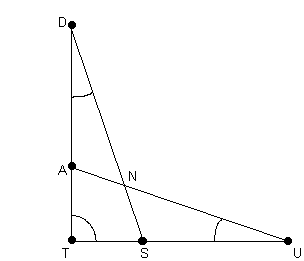Vorausetzung:  und  = 

Behauptung:  = 

Beweis:

Aussage: Begründung:

1.) 

2.) laut Voraussetzung

3.) Die beiden Dreiecke DTS und ATU

haben denselben Winkel 

4.) folgt aus 1.) 2.) und 3.) wenn man den

WSW - Satz anwendet

5.)  = 

6.)  +  = 

+  = 

7.) folgt durch Umformung von 6.)

8.)  =  - 

9.)  = 

Lösung:

Aussage: Begründung:

1.)  laut Voraussetzung

2.)  =  laut Voraussetzung

3.) Die beiden Dreiecke DTS und ATU siehe Figur

haben denselben Winkel 

4.)  DTS   ATU folgt aus 1.) 2.) und 3.) wenn man den

WSW - Satz anwendet

5.)  =  folgt aus 4.)

6.)  +  =  siehe Figur

+  = 

7.)  =  -  folgt durch Umformung von 6.)

=  - 

8.)  =  -  wegen 2.) kann man  durch  ersetzen wegen 5.) kann man  durch  ersetzen

9.)  =  folgt aus 7.) und 8.)

8.: In der folgenden räumlichen Figur ist die Strecke [A,D]  [U,D] und es gilt weiter [A,D]  [D,I]. Die Winkel  und  sind gleich groß.

Begründe, daß  =  ist !

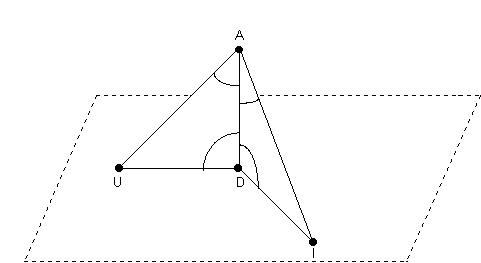
Lösung:

[A,D]  [U,D] laut Vorausetzung, daraus folgt ADU = 

[A,D]  [D,I] laut Vorausetzung, daraus folgt ADI = 

Weiters gilt  und aus der Figur kann man entnehmen, daß die beiden Dreiecke ADU und ADI eine Seite - nämlich AD - gemeinsam haben. Daraus folgt mit Hilfe des WSW - Satzes, daß die beiden Dreiecke kongruent sind.

Weiters folgt, daß auch die Winkel bei I und U gleich groß sein müssen. Also sind die beiden Dreiecke kongruent und somit sind auch alle drei Seiten gleich lang. Insbesondere gilt  = .

Gegeben:  =  ,  und .

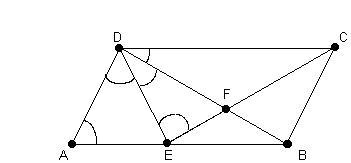Lösungversuche:

1.Behauptung: DEF  CBF. Diese Behauptung kann mit den gegebenen Voraussetzungen nicht begründet werden.

2.Behauptung: DEB  CBE. Auch diese Behauptung kann mit den gegebenen Voraussetzungen nicht begründet werden.

3.Behauptung: ADB  EDC.

Begründung:

Laut Voraussetzung ist . Aus der Figur kann man entnehmen, daß

der Winkel ADB =  und der Winkel EDC =  ist. Da laut Voraussetzung  ist, kann man  durch  ersetzen und erhält, ADB =  = EDC . Weiters gilt laut Voraussetzung, daß  =  und  ist. Also haben die beiden Dreiecke ADB und EDC zwei gleich große Winkel und eine gleich lange Seite und daraus folgt mit Hilfe des WSW - Satzes, daß die beiden Dreiecke kongruent sind.

10.: In der folgenden Figur ist LT die Winkelsymmetrale des Winkels ULP und LP die Winkelsymmetrale des Winkels TLI. Weiters gilt:  und  = .

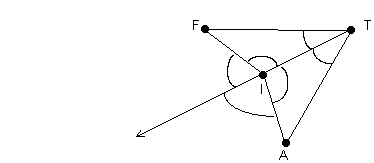
Begründe, daß  TUL   PIL ist !

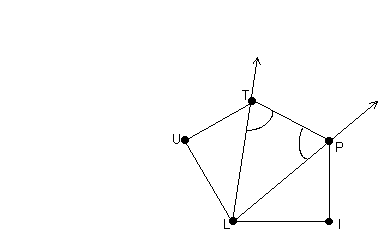
Lösung:

LT ist die Winkelsymmetrale des Winkels ULP. Daraus folgt:

ULP =  ULT +  TLP, wobei  TLP =   ULP und  ULT =   ULP

LP ist die Winkelsymmetrale des Winkels TLI. Daraus folgt:

TLI =  TLP +  PLI, wobei  TLP =   TLI =   ULP =  ULT

Daraus folgt, daß die drei Dreiecke TUL, TLP und PIL jeweils einen gleich großen Winkel haben.

Weiters gilt laut Voraussetzung, daß  ist. Daraus folgt, daß das Dreieck TLP ein gleichschenkeliges Dreieck ist. Es gilt also:  = 

Laut Voraussetzung ist  = .

D.h. die beiden Dreiecke TUL und PIL haben zwei gleich lange Seiten und einen gleich großen Winkel. Daraus folgt mit Hilfe des SWS - Satzes, daß die beiden Dreiecke kongruent sind.